Базовые структуры данных.

Продолжаем тему CS. В этом посте разберем базовые структуры данных, такие как: массив, связный список и стек.

1. Массив

Массив - структура данных, в которой элементы хранятся в памяти друг за другом. Для того, чтобы они не перезаписали другую информацию, массив имеет постоянный размер, который указывается при инициализации. Благодаря этому мы можем легко получить доступ к любому элементу массива по индексу за константное время. Адрес ячейки с нужным элементов можно будет найти по формуле p = a + b * c , где a - адрес начала массива, b - размер одного элелмента элемента и с - индекс нужного элемента. Это значит, что массив является структурой данных с произвольным доступом.

Примеров на Java и C++:

int a[] = {1,2,3,4,5}; // Эта строка и весь код создают одинаковый массив
int b[] = new int[5];
b[0] = 1;
b[1] = 2;
...
...
b[4] = 5;

b[5] = -1; // Вызовет ошибку выхода за пределы массива, т.к. размер массива 5,а мы пытаемся добавить 6-ой элемет

int a[5] = {1,2,3,4,5};

int b[] = {1,2,3,4,5};

int c[5];
c[0] = 1;
c[1] = 2;
...
...
c[4] = 5;

1.1 Динамические массивы

Что же делать если мы не знаем при создании, сколько элементов нам придется хранить? Для такого случая используются динамические массивы. Единственное отличие их от обычных массивов в том, что при попытке добавить элемент, для которого нет места, создается новый массив с большим размером, в который копируется весь первоначальный массив и добавляется элемент. Естественно, это плачевно сказывается на скорости.

1.2 Сложность действий над массивом

	Массив	Динамический массив
Доступ к элементу по индексу	O(1)	O(1)
Поиск элемента	O(n)/Ω(1)	O(n)/Ω(1)
Добавление элемента в конец массива	O(1)	O(n)/Ω(1)
Добавление элемента в начало/середину массива	O(n)	O(n)
Удаление элемента	O(n)/Ω(1)	O(n)/Ω(1)

Про доступ по элементу и почему он такой быстрый мы говорили выше.

Поиск элемента так же затрагивался в посте про сложность алгоритмов, но повторим. Допустим у нас есть массив [1,2,3,4,5]. Для поиска нам необходимо пройтись по массиву один элемент за другим, сравнивая их с искомым. В худшем случае мы будем искать элемент, которого в массиве нет и чтобы понять это, нам надо пройти все N элементов, где N - размер массива. Больше массив, дольше поиск. Конечно в лучшем случае, мы будем искать первый элемент (в нашем случае 1) и за констатное время получим результат.

Добавление элемента в конец занимает констатное время, если в массиве есть место. В случае с обычным массивом, у нас нет случая, когда массив заполнен. Из-за этого вставка в конец (если она возможна) занимает O(1). В динамическом массиве пока есть место вставка так же будет занимать O(1), однако, как только место закончится, нам придется пройти через весь оригинальный массив и по одному копировать элементы в новый массив, что займет линейное количество времени.

Вставка в начало или середину массива занимает больше времени, т.к. нам необходимо сначала подвинуть все элементы, которые идут в вставляемой ячейке и после нее, чтобы сделать место для нашего элемента.

Удаление элемента требует так же линейное время, т.к. после удаления, нам необходимо сдвинуть элементы массива после удаленного на один шаг.

Моя реализация динамического массива на C - https://github.com/mrZizik/coding_practice/tree/master/C/dynamic_array

2. Cвязный список

Мы всегда создаем массив большего размера, чем количество данных хранящихся в нем. Так же массив имеет фиксированный размер и добавление большего количества элементов или невозможно или требует больших затрат по времени. Решить обе эти проблемы может связный список.

Свя́зный спи́сок — базовая динамическая структура данных в информатике, состоящая из узлов, каждый из которых содержит как собственно данные, так и одну или две ссылки («связки») на следующий и/или предыдущий узел списка.

Linked list

Как мы видим на картинке и читаем в определении, связный список состоит из узлов или нод. Каждая нода содержит в себе сам элемент и ссылку на следующий. Сам список хранит ссылку на первый узел (head) и количество элементов. В некоторых случаях связный список так же содержит ссылку на последний элемент и каждая нода хранит ссылки на предыдущий. Такой список называют двусвязным. Благодаря наличию указателей в каждом узле, элементы могут распологаться случайным образом в памяти и нам нет необходимости заранее ее занимать. Так же, благодаря узлам, нам не надо передвигать все элементы, для добавления нового в начало или середину списка и удаления какого-либо элемента. Мы просто меняем наши указатели нужным образом.

Плюсы связного и двусвязного списков мы уже знаем:

динамическое добавление элементов без ограничения по памяти
отсутствие необходимости в инициализации лишних элементов списка.

Как и у любой структуры данных, у связного списка есть минусы:

медленный доступ по индексу. Мы не можем, как в массиве за константное время достать i-ый элемент
расход памяти на хранение ссылок в узлах

Пример работы с связным списком в Java:

       LinkedList<String> linkedlist = new LinkedList<String>();

       linkedlist.add("A");
       linkedlist.add("B");
       linkedlist.add("C");
       linkedlist.add("D");
       linkedlist.add("E");

       linkedlist.addFirst("AA");
       linkedlist.addLast("ZZ");

       linkedlist.addFirst("AA");
       linkedlist.addLast("ZZ");

2.1 Сложность действий над связным списком

	Связный список	Двусвязный список
Доступ к элементу по индексу/Поиск элемента	O(n)/Ω(1)	O(n)/Ω(1)
Добавление/удаление элемента в середине	O(n)	O(n)
Добавление/удаление элемента в начале	O(1)	O(1)
Добавление/удаление элемента в конце	O(n)	O(1)

Имлпементация связного списка:

C - https://github.com/mrZizik/coding_practice/tree/master/C/linked_list
Python - https://github.com/mrZizik/coding_practice/tree/master/python/linked_list

3. Стек

Стек, наверное, одна из самых простых структур данных. Это список построенный по принципу LIFO (Last In, First Out) или на русском последний зашел, первый вышел. Легче всего его представить в виде детской пирамидки. Мы можем насаживать на стержень кольца по одному и можем достать самое верхнее кольцо. Однако мы не можем получить доступ к кольцам ниже самого верхнего.

В основном над стеком можно совершить только два действия:

push - положить что-то на вершину стека
pop - забрать что-то с вершины стека.

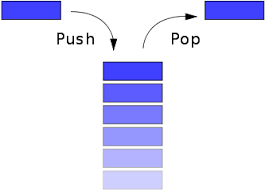
Stack

Дополнительно в некоторых реализациях у него имеются методы вывода размера, печати всего стека или чтения элемента с вершины оставляя сам стек неизменным.

Несмотря на такую простоту и ограниченность, стек идеально подходит для решения многих задач. Одной из таких является проверка скобок на закрытие в разных IDE. Увидев открывающую скобку, она добавляет ее на стек, найдя же закрывающую она проверяет находится ли на вершине стека парная скобка и удаляет ее. Если пройдя весь код, стек оказывается пустым, значит все скобки стоят правильно и имеют свои пары.

Пример работы с связным списком в Java:

       Stack<String> stack = new Stack<>();
       stack.push("A");
       stack.push("B");
       stack.push("C");

       String element = stack.pop();

Стек можно имплементировать поверх связного списка или динамического массива. В обоих случаях и push и pop выполняются за константное время O(1). В случае с массивом, для ускорения нам надо будет допустить, что основанием стека будет начало массива и вершиной конец. В таком случае добавление и удаление элементов в конец массива будет быстрее, т.к. не надо будет каждый раз сдвигать все элементы массива.

Имплементация стека:

C (поверх массива) - https://github.com/mrZizik/coding_practice/tree/master/C/stack_array

Written on September 24, 2018