Первый “конспект” для повторения Computer Science основ.

Сложность алгоритмов

Вычисли́тельная сло́жность — понятие в информатике и теории алгоритмов, обозначающее функцию зависимости объёма работы, которая выполняется некоторым алгоритмом, от размера входных данных. (c) Wikipedia

Если повторить тоже простыми словами, сложность показывает насколько растет количество операций в алгоритме в зависимости от количества инпута. Например, говорят, сложность алгоритма сортировки пузырьком O(n^2), где n это количество элементов в массиве. То есть на сортировку массив с размерностью 10, нам необходимо 100 операций (мы сравниваем каждый элемент со всеми). Опять же надо понимать, что это не говорит нам быстрый алгоритм или нет и насколько быстро в единицах времени он выполнится. На одной машине он может выполнится за одно время, на другом за другое.

O, Ω, Θ - нотации

Допустим у нас есть массив [3, 8, 1, 5, 7]. Нам необходимо найти в нем элемент. Для этого нам придется пройти по всему массиву (5 операций). Но если элемент, который мы ищем это “3”, то тот же алгоритм завершит поиск на первом шаге. Для обозначения сложности в худшем случае и лучшем используются O и Ω нотации. Для случая выше алгоритм имеет сложность O(n) и Ω(1).

Немного математики за нотациями.

Назовем функцию, которая определяет количество шагов на выполнение алгоритма f(x). Возьмем другую простую функцию g(x).

O

f(x) принадлежит O(g(x)) (алгоритм имеет сложность O(g(x))) тогда и только тогда, когда f(x) <= C * g(x), при x>X и C>0.

Это значит, что количество шагов будет расти медленнее или как минимум так же, как и g(x). Пример на алгоритме выше. Поиск никогда не займет больше O(n) операций, т.к. в самом худшем случае мы пройдем все 5 элементов. Но может случиться так, что мы найдем нужный элемент раньше, чем пройдем все элементы.

Ω

f(x) принадлежит Ω(g(x)) (алгоритм имеет сложность O(g(x))) тогда и только, когда f(x) >= C * g(x), при x>X и C>0.

Тут все наоборот: количество операций будет расти быстрее или как минимум так же, как и g(x). Поиск в том массиве никогда не будет быстрее 1 шага, т.к. в самом лучшем случае мы найдем нужный элемент первым. Но это не исключает, что нам придется пройти и второй и третий и весь массив. Значит алгоритм имеет сложность Ω(1).

Θ

f(x) принадлежит Θ(g(x)) (алгоритм имеет сложность O(g(x))) тогда и только, когда f(x) принадлежит и O(g(x)) и Ω(g(x)), при x>X и C>0.

Количество шагов растет так же, как и g(x). Например достать элемент из массива по индексу. В лучшем случае вы запросите элемент по индексу и получите за 1 операцию. В худшем случае вы запросите элемент по индексу и опять же получите за 1 операцию. Алгоритм имеет сложность Θ(1)

Чаще всего встречается O-нотация, т.к. нам интересно, как поведет себя алгоритм в худшей ситуации.

График сложностей алгоритмов

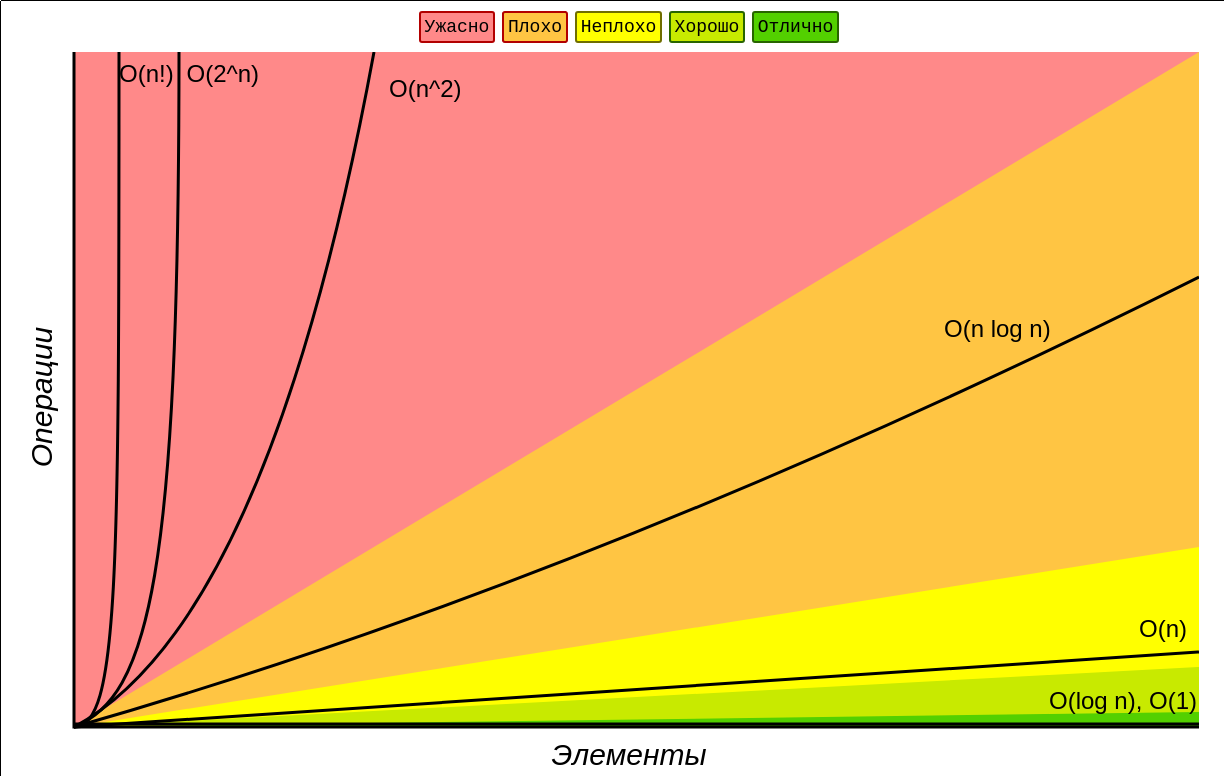
На графике видно, что самые быстрые алгоритмы имеют сложность O(1) и самые медленные O(n!).

• http://bigocheatsheet.com/ - Хорошая шпаргалка по сложностям
• https://www.youtube.com/watch?v=V6mKVRU1evU - Видеолекция с упором на математическую составляющую
• https://www.youtube.com/watch?v=V6mKVRU1evU - Короткое объяснение сложности алгоритмов